努力賺錢的 Tsum Tsum 玩家們一定都曾經好奇過:
到底什麼時候才是開道具的好時機?
台輟看了坊間各式各樣的說法,都不見一個完整且有正確根據的答案。那好吧,咱們自己來算!跟著算完,相信你以後就能判斷該不該開道具咯。
前提
「+coin」道具的期望值
為了量化「+coin」的效益,我們首先得知道「+coin」平均帶來的加成效果是多少。
這部分官方並沒有給資料,但好在有個日本網友實測了 1000 場,將數據刨了出來,原文表格如圖:
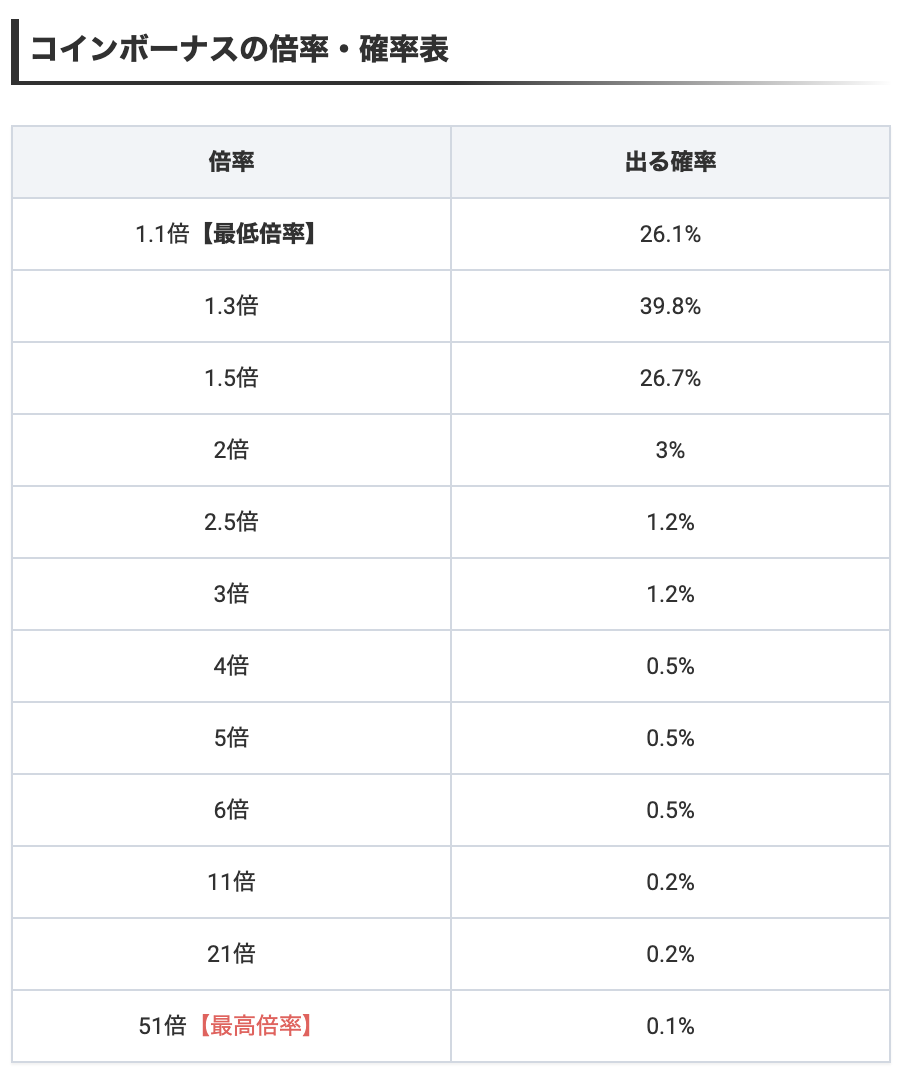
有了數據,我們就可以算出「+coin」的加成期望值為:
1.1×26.10%+1.3×39.80%+1.5×26.70%+2×3%+2.5×1.2%+3×1.2%+4×0.5%+5×0.5%+6×0.5%+11×0.2%+21×0.2%+51×0.1%=1.521
這個數字將會是很重要的計算依據。
設定參數
為了方便後文撰寫,此處設
- A = 什麼道具都不開長期平均結算的錢
- B = 單開「5變4」長期平均結算的錢(未計算成本)
我們再考慮到上述「+coin」的期望值可以得到:
- 1.521A = 單開「+coin」長期平均結算的錢(未計算成本)
- 1.521B = 雙開「+coin」跟「5變4」長期平均結算的錢(未計算成本)
狀況 1:何時應該開「+coin」?
根據前提,我們知道 1.521A 為單開「+coin」長期平均結算的錢。我們用它來計算看看什麼時候應該開。
{1.521A−500>0(計算成本後不能虧錢)1.521A−500>A(開「+coin」計算成本後要比不開賺得多)
計算後得(其實因為 A 本來就恆正,所以根本不用算上式啦)
{A>328.73109796(計算成本後不能虧錢)A>959.69289827(開「+coin」計算成本後要比不開賺得多)
求交集得
A>959.69289827
結論 1
如果你「什麼道具都不開長期平均結算的錢」大於 960,那單開「+coin」就比「什麼都不開」好。
例子
-
如果不開「+coin」平均每場賺的錢是 500,那麼開了就是:500×1.521−500=260.5(變少了)
-
如果不開「+coin」平均每場賺的錢是 1000,那麼開了就是:1000×1.521−500=1021(變多了)
-
如果不開「+coin」平均每場賺的錢是 2000,那麼開了就是:2000×1.521−500=3042−500=2542(變多了)
狀況 2:何時應該開「5變4」?
這題就相對很簡單了,計算如下:
{B−1800>0(計算成本後不能虧錢)B−1800>A(開「5變4」計算成本後要比不開賺得多)
因為 A 恆正,我們求交集可以得到結論:
B−A>1800
非常直觀,這個不用算都知道對吧!
結論 2
當「單開『5變4』長期平均結算的錢」比「什麼道具都不開長期平均結算的錢」多出 1800以上,此時單開「5變4」就比「什麼都不開」好。
例子
如果本來一場平均只能賺 1000,但開「5變4」後一場平均可以賺 2800 以上,那一直開的效益就是正的。
狀況 3:何時可以雙開「+coin」跟「5變4」?
「+coin」道具跟「5變4」道具雙開的情形就比較複雜了。因為雙開的意義是——我不止希望有賺,我還希望我雙開後的效益比單開來得更高。
據此,我們可以列式如下:
⎩⎨⎧1.521B−2300>0(計算成本後不能虧錢)1.521B−2300>1.521A−500(雙開必須大於單開「+coin」)1.521B−2300>B−1800(雙開必須大於單開「5變4」)
計算後得
⎩⎨⎧(B−A)>1183.43195266B>959.69289827B>1512.16305062
求交集得
{(B−A)>1183.43195266B>1512.16305062
結論 3
當「單開『5變4』長期平均結算的錢」大於 1513,且「單開『5變4』長期平均結算的錢」比「什麼道具都不開長期平均結算的錢」多出 1184以上,此時雙開會比單開好!
集大成!
至此,我們集結了三個結論:
- 結論 1:如果你「什麼道具都不開長期平均結算的錢」大於 960,那單開「+coin」就比「什麼都不開」好。
- 結論 2:當「單開『5變4』長期平均結算的錢」比「什麼道具都不開長期平均結算的錢」多出 1800以上,此時單開「5變4」就比「什麼都不開」好。
- 結論 3:當「單開『5變4』長期平均結算的錢」大於 1513,且「單開『5變4』長期平均結算的錢」比「什麼道具都不開長期平均結算的錢」多出 1184以上,此時雙開會比單開好!
實戰演練 1
如果什麼都不開就能平均賺 2000,開了「5變4」後平均賺 3000。那麼此時只滿足了結論 1,所以此時單開coin就好! 我們實際算算看:
-
只開「+coin」每場能淨賺 2000×1.521−500=3042−500=2542(勝出)
-
只開「5變4」每場能淨賺 3000−1800=1200(虧了)
-
雙開每場能淨賺 3000×1.521−2300=4563−2300=2363(有賺但不如單開「+coin」)
實戰演練 2
如果什麼都不開就能平均賺 2000,開了「5變4」後平均賺 3200 呢?
此時滿足結論1、3,代表單開「+coin」會賺,但雙開會更賺!我們實際算算看:
- 只開「+coin」每場能淨賺 2000×1.521−500=3042−500=2542(有賺但不如雙開)
- 只開「5變4」每場能淨賺 3200−1800=1400(虧了)
- 雙開每場能淨賺 3200×1.521−2300=4867.2−2300=2567.2(勝出)
迷思破除
雙開道具「多賺的錢」(也就是1.521裡面的0.521)可以超過成本(500+1800)就一定不會虧?我們討論看看:
這個一定不會虧的情形列成式子就是
0.521x>2300
可以算得 x>4414.58733 ,所以得出「能賺超過 4415 就一定不會虧」的結論。
但是,以上式子展開來看他的底層邏輯其實長這樣:
1.521x−2300>x
意思是,雙開後賺的錢扣掉成本會⋯⋯大於只開「5變4」但是不用扣成本?Bug就出現了,其實不太正確。
聽理論不如直接舉一個反例:
假設我今天開「5變4」可以賺 5000,但其實不開「5變4」就已經能賺4000了(有些角色確實有這樣的特性,例如加斯頓,對吧?),算算看是不是真的不虧:
- 雙開後,平均每場可以賺 5000×1.521−2300=5305
- 單開「+coin」,平均每場可以賺 4000×1.521−500=5584
這裡單開才是賺更多錢的作法。相對的,雙開虧了(根本不該開「5變4」)。
換一個方面再舉一個反例:難道只賺3000,雙開就虧了嗎?
這一樣要看開跟不開的差距而定。舉一個還算常見的情形好了。假設不開「5變4」能賺 1000 ,開了能賺 3000。
- 雙開後,平均每場能賺 3000×1.521−2300=2263(注意,這裡的 2263 依舊比單開「5變4」的 3000-1800=1200還多,並沒有虧喔)
- 單開「+coin」則是平均每場能賺 1000×1.521−500=1021
此時當然要雙開啊,一點都不虧!